How Machine Learning Can Transform the Drug Development Pipeline
- by Stefan Schroedl, Head of Machine Learning at Atomwise
Originally posted on Medium
This post is intended for my fellow machine learning engineers who are curious about applications in medicine, biology, or chemistry, but without a prior formal background in these fields. I have been in this position myself; my goal in this post is to give you a concise starting point into the field of drug discovery.

In the first part, I sketched the “what” of machine learning in drug discovery: its objectives and role within the drug research pipeline, types and quality of experimental data, benchmarks and evaluation metrics. That set the scene for the present post, where we are going to explore the “how” of actual approaches in greater detail. Unfortunately space does not permit a complete coverage of the rather large body of literature; I apologize in advance for subjectively leaving out some works and references. Nevertheless, I am going to discuss a number of prototypes that span the spectrum of approaches that have been developed so far. In case you are wondering, there won’t be a final conclusion of what is “best”; as mentioned in the first part, it is often difficult to compare results apple-to-apple, and I will refer you to the original papers instead to form your own opinion.
Multiple axes exist along which the exposition could be organized, such as historical development or the type of machine learning technique. Another major categorization is whether a method is ligand-based or able to generalize across targets. However, the most distinguishing characterization appeared to me to be that of data representation, which I will take as the guiding principle. Most traditional machine learning and statistical data analysis techniques operate on feature vectors of fixed dimension. Proteins and molecules are of course of variable size, characterized by a connectivity pattern through covalent bonds, and by a spatial structure which is crucial for their interactions. We will walk through different chemical representation schemes, in order of increasing complexity.
First, a quick side note on software: If you want to start playing with molecular representations and algorithms yourself, there are several open source and commercial packages available that make it easy to read, write, convert, and process chemical data. Openbabel is geared towards handling various different file formats and flavors of data. The de facto industry standard for representing chemical structures is a format called molfile, for single molecules, and SDF (Structure-Data File) for multiple molecules and associated metadata. It is basically a fixed-width format where each line describes an atom with its coordinates or one bond. Rdkit is a versatile and popular Python cheminformatics library which offers functions for calculation physical properties, energies, and fingerprint calculations.UCSF Chimera and pymol can read SDF files and visualize proteins and molecules graphically.
DeepChem is an integrated python library for chemistry and drug discovery; it comes with a collection of implementations for many of the machine learning algorithms I am going to talk about. Associated with it is the benchmark set MoleculeNet.
Molecular Representations
1-D Descriptors
There are a handful of experimental and calculated molecular properties that are often used for rough classifications: molecular weight, solubility, charge, number of rotatable bonds, atom types, topological polar surface area, and so on. Since these scalar attributes do not take into account a molecule’s bond structure, we will call them here one-dimensional.
Long before computers or machine learning even existed, chemists were interested in predicting chemical reaction rates and physical properties. They used to fit simple regression models. But in fact, machine learning is really a glorified description of curve fitting with the help of computers. From this point of view, it is hard to say when machine learning for chemistry started historically, as it is a just a natural progression of these early quantitative models.
In some cases, simple models actually work remarkably well. Take for example a property called the partition coefficient, or logP, which measures the ratio of solubilities in two different substances. Perhaps surprisingly, an (almost) chemically accurate linear model has been developed (termed computed logP, or cLogP) that operates by summing up atom- or fragment-specific constants for all constituents of a molecule. Similar results have been achieved early for predicting certain reaction rates (if you are curious, look up theHammett equation).
These properties still seem a long shot away from drug development. On the other hand, of course, we could not hope to meaningfully address the latter without the former. Also, as mention above, real medicines must fulfill a number of other requirements apart from pure binding affinity. By whatever route they are administered, they must exhibit at least limited aqueous solubility for therapeutic efficiency. The Lipinski rule of 5 is an astonishingly simple rule of thumb that is often used to pre-filter drug candidates (to be chemically accurate, there are actually 3 rules containing 5's, and 1 rule containing a 10).
2-D Descriptors
When chemists talk about a two-dimensional descriptor of a molecule, what they mean is taking into account the graph of covalent and aromatic bonds, but not spatial coordinates. This is a molecule as it can be drawn on a sheet of paper. This figure shows the structure of imatinib, a targeted therapy for leukemia and one of the first drugs by “rational design”:

Imatinib structural graph
A common way of mapping variably structures molecules into a fixed-size descriptor vector is “fingerprinting”. Multiple such methods have been developed. Some are based on expert-derived features (e.g., number of specific types of bonds, hydrogen bond donors or acceptors). But circular fingerprints are in more widespread use today. Here, each atom is inspected together with its neighborhood of bonded atoms at distance 1, 2, …; instead of pre-defined chemical concepts, each of such local patterns switches on one bit according to a hash function. A typical size of the bit vector is 1024. One standard implementation are extended circular fingerprints (termed ECFPx, with a number x designating the maximum diameter; e,g, ECFP4 for a radius of 2 bonds). The similarity between two molecules can be estimated using the Tanimoto coefficient (the same metrics is known in other domains as Jaccard index) — the number of bits set to one in both molecules, divided by those in either one. Database similarity searches were the original motivation for circular fingerprints, as they can be implemented very efficiently through bitwise operations. But they later also helped to flexibly extend the number of molecule features for machine learning; the above-mentioned dozens or so of 1-D properties alone obviously go only so far.
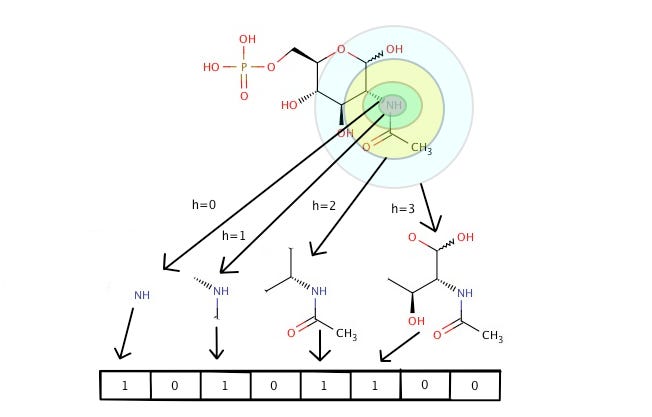
Now such an encoding is necessarily non-unique — it is possible that two completely different molecules are hashed to the same fingerprint. This can sometimes be a point of confusion — how can machine learning still work without making gross mistakes? But there is some guard against this in generally having enough bits set; indeed, hash collisions can even be seen as a welcome measure to prevent overfitting. The argument is exactly analogous to the introduction of feature hashing in the context of machine learning for text applications.
QSAR
Most pharmaceutical projects focus on a single or a handful of targets at a time. In this case, the protein(s) can be assumed to be more or less fixed; as a consequence, we can restrict ourselves to features of the molecule. Starting in the 1960’s and 1970’s, medicinal chemists started applying such ligand-based approaches, mostly linear and logistic regression models on 1-D features, fitting experimental assay data for potency and toxicity of potential new drug molecules. This was termedquantitative structure-activity relationship (QSAR).The basic premise is that limited modifications of molecules lead to small changes in physical properties or binding affinities. This is often true but sometimes dramatically wrong, in which case it is called an “activity cliff”.
For decades now, fingerprint features have been one of the pillars of QSAR methods, and they are still quite effective tools. There have been many variants and refinements of this approach. One direction of generalization aims at capturing information from multiple targets(a list of proteins fixed in advance). Imagine a matrix with columns labeled by proteins, and rows by compounds. This table is obviously huge and can only be filled sparsely with experimental data. However, certain families of proteins, such as kinases, have a peculiar and distinctive way of binding ligands, and we can hope to capture and transfer knowledge across the group. This setup reminds of e.g. collaborative filtering for movie recommendation, with movies (resp. users) taking the role of targets (compounds). The profile-QSAR method [Martin et al, 2017] first uses ligand-based, target-specific fingerprint models to fill in the matrix; then, it trains a global partial least squares model on top of the matrix for extrapolation to previously unseen kinases and compounds.
Multi-Task Neural Networks
A similar setup — a matrix of targets and compounds, represented as fingerprints — was pursued when Kaggle hosted the 2012 Merck Molecular Activity Challenge. It sparked the research in this field and also captured a lot of attention in the popular media. Multi-task prediction here means regarding each of a predefined number of target proteins as a separate task. Note that this still conforms to the definition of a ligand-based method, as no explicit protein features are included. The winning team from the University of Toronto used a fully-connected multi-task neural network that was later developed further [Dahl et al, 2014]. The advantage over single-task models consists in the possible sharing of common information. This is in analogy to image processing, where the lowest convolutional network layers learn to recognize corner and edge features that are essential regardless what type of objects ultimately need to be discriminated. The deep neural network solution was an impressive success both in terms of technological advancement and public awareness. Unfortunately, the approach is not directly applicable in practice, due to the way the problem was framed for this competition. Typically, experimental knowledge of the drug-target matrix is extremely sparse; and nothing can be inferred from it for novel targets.
Graph Convolution
On a high level, the algorithm to generate circular fingerprints can be described as follows. Each atom is visited in turn, in arbitrary order; a function of its properties (e.g., atom type) and its immediate neighborhood is computed, and hashed into a bit vector. Fingerprints for larger patterns, say of diameter 4, can be constructed by two such propagation steps, the only difference being that the second step is acting on the output of the first one, instead of the original atom representation. After each step, the outputs for all atoms are jointly hashed into the same bit vector.
Neural fingerprints [Duvenaud et al, 2015]were proposed as a differentiable and hence learnable generalization of this pattern. The hash function is replaced by a neural network; the final fingerprint vector is the sum over a number of atom-wise softmax operations, in a way similar to the pooling operation in standard neural networks. By connecting a neural fingerprint network to a standard fully connected network, the representation can adapt to the task at hand and reflect characteristics of the input chemical space in a more smooth and suitable way than fixed, predefined circular fingerprints.
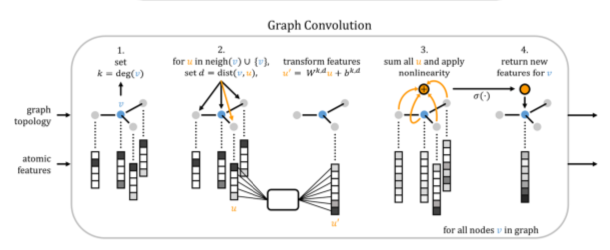
This concept has been refined in several different ways. Kearnes et al [2016] applied 2-D graph convolutions to a number of ligand-based drug discovery benchmarks. [Gilmer et al, 2017] recognized that several of such approaches could be described uniformly in the framework of neural message passing. It can also be seen as a generalization of the usual understanding of convolution to graphs. We associate a fixed-dimensional node embedding vector with each atom, which can be initialized by any known properties, such as the atom type, charge, or number of bonds. Then, it receives messages from its neighbors. The form of these messages varies, but it is a function of neighbor states, edge types, and possibly distance information. Atom state vectors are updated from their previous states and the received messages. In some instantiations, edges can have learnable states as well. The propagation process is repeated either a fixed number of times, or until some convergence criterion is met. Finally, a single output value has to be computed from the set of atom state vectors. In the simplest case, this can be done by an arithmetic reduction (e.g., addition). In order to restrict the loss of information, Kearnes [2016] collapsed individual components of the atom vectors to smoothed histograms. The set2set approach [Gilmer et al, 2017] is another more powerful way of combination. Alternatively, the reduction step can be side-stepped completely by designating one unique pseudo-atom to hold the overall result.
Auto-encoders
Another line of research based aims at finding compact latent representations. An embedding converts discrete representations of molecules to and from a multidimensional continuous representation. This can subsequently be used to preserve local similarities in a task-dependent way; it can also enable generative networks to design compounds with certain target properties. Latent representations can be trained on unlabeled data in an unsupervised or semi-supervised fashion; often, unlabeled examples are available in much larger numbers than labeled ones. Even without target information, they are still useful to convey information about the background distribution of the chemical space of the application.
An auto-encoder is an encoder-decoder pair trained to minimize error in reproducing the original input, i.e., attempting to learn the identity function. Key to the design is an information bottleneck, a learned compressed representation that captures the most statistically salient information in the data. A recent publication [Kadurin et al, 2016] features an adversarial auto-encoder. Its input consists of of a circular fingerprint of a molecule that was tested in an assay, together with the respective concentration. The special twist is that the latent layer additionally contains a supervised node for the observed biological activity. After finishing the training phase, the network samples latent representations without input to generate fingerprint-like features and concentrations. A number of those outputs with low concentrations (i.e., high potencies) are selected as keys for a similarity search of actual molecules in Chembl. These could be chemically verified to have good biological activity.

So far, we have focused on circular fingerprint representations. Let’s switch gears now and look at an orthogonal formalism called SMILES (“Simplified molecular-input line-entry system”). It represents molecules in the form of ASCII character strings. There are usually several equivalent ways to write the same compound (and at different level of detail, such as specifying isomers). The lack of unique identifiability of molecules is a weakness, but on the other hand, SMILES are reasonably human-readable. The SMILES string for out friend molecule imatinib is:
CC1=C(C=C(C=C1)NC(=O)C2=CC=C(C=C2)CN3
\CCN(CC3)C)NC4=NC=CC(=N4)C5=CN=CC=C5
When applying neural networks to this formalism, researchers naturally converge on network types most suitable for sequence data, such as recurrent neural networks and LSTM (Long/short term memory) networks. We have sketched the use of circular fingerprints for (variational) auto-encoders, but SMILES can be used as well. Xu et al [2017] report results on the prediction of 1-D properties of molecules that outperform the corresponding fingerprint-based approach. Gómez-Bombarelli et al [2018] attempt to optimize a target property of a molecule by gradient descent in the continuous space of a latent embedding, rather than in the discrete space of the primary (SMILES) representation. In this application, the variational auto-encoder is based on a recurrent neural network. An initial molecule is selected and fed to the network. Its encoded latent vector forms the starting point for the network to move in a direction most likely to improve the desired attribute. The resulting new candidate vector can then be decoded into a corresponding molecule.
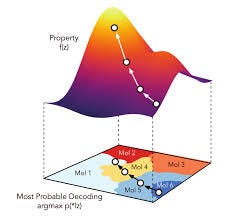
Molecule optimization in latent space.
One major drawback with SMILES-based generative approaches is that not every possible output string corresponds to a valid, synthesizable molecule. Sanchez-Lengeling et al [2017] refined the generative approach for an adversarial network: Validity is enforced through a discriminator network whose feedback is combined linearly with the desired molecule property into a joint objective function for the generator network.
This concludes my overview of machine learning methods based on 2-D representations. Let us now explore one more dimension.
3-D (structural) methods
Fingerprints and SMILES describe the bond structures of molecules. But most small molecules can adopt multiple 3-D conformations which can be more or less favorable, depending on their context. Thus, 2-D representations do not convey the complete information. The following diagram illustrates two possible conformations of ethane:
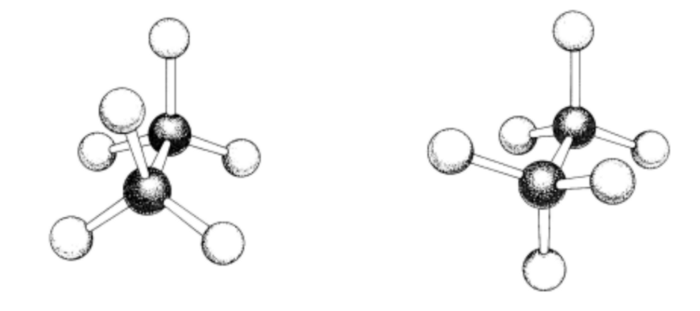 >This is a very simple molecule; but note that the number of such possible conformations grows exponentially with the number of rotatable bonds. Here is a spatial stick-and-ball illustration of our drug molecule imatinib:
>This is a very simple molecule; but note that the number of such possible conformations grows exponentially with the number of rotatable bonds. Here is a spatial stick-and-ball illustration of our drug molecule imatinib:
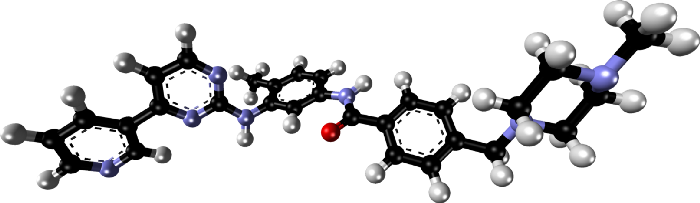
Ultimately, the action of a drug must manifest itself through physical interactions between its atoms and those protein atoms that are in close range of them. Therefore, researchers have been striving to reveal spatial and chemical interactions for guidance in drug development.
In the late 1980’s and 1990’s, a widely used precursor 3-D QSAR approach was called comparative molecular field analysis (Comfa; [Cramer et al, 1988]). This was still a ligand-based method, but it tried to develop a three-dimensional grid model of the spatial force field induced by a compound. First, candidate molecules are aligned to a common template. Classical force fields on a hypothetical probe hydrogen atom are estimated at each grid point, and concatenated into a flat vector of QSAR features. Since the number of such features can easily exceed the training set size, there is a risk of overfitting. To prevent this, the partial least squares method is used with a lower number of latent features. Subsequently, PLS became and has stayed a popular go-to method in the chemistry domain, since it applies feature induction and induction in one step.
So far, we have only talked about featurizations of the ligand. But if we ever want a model to be able to generalize to previously unseen targets, or to train it to learn physical concepts underlying a drug mechanism, we will need to extract features for the protein as well. It is less clear how to do that meaningfully through 2-D representations as in the case for for ligands: They are orders of magnitude larger, consisting of long chains of amino acids, each of which in turn consists of many atoms (19.2 on average). In general, only a handful of amino acids participate in the interaction with a ligand. Since the protein is folded up in complex ways, amino acids that are physically close to each other, or to the ligand, don’t necessarily have to be close within the sequence.
It has indeed been tried to extend 1-D and 2-D approaches to proteins. For example, [Lenselink et al, 2017] split the amino acid sequence into 20 equal subsegments (whose individual length depends on the total protein length); each such segment is summarized by taking averages over amino acid properties (molecular weight, charge, hydrogen bond acceptors and hydrogen bond donors, etc). Maybe surprisingly, this representation did manage to glean usable information from the protein. While this proved to be a viable approach, it is however clear that ad-hoc, whole-sequence featurizations will be inherently limited.
In summary, for further progress the spatial interaction with the protein has to be taken into account. You might have heard talk of the protein folding problem as a holy grail of science: to predict ab initio how the string of amino-acids takes on its characteristic three-dimensional shape. Due to its immense difficulty, most structures need to be elucidated experimentally through physical and chemical methods, most importantly X-ray crystal diffraction; in recent years, NMR and cryo-electron-microscopy have started to make inroads as well. Structure determination can be painstaking work taking months. Often the most difficult step is to purify and crystallize enough substance. Some important classes such as GPCRs are notoriously hard; as membrane proteins, they contain alternating hydrophilic and hydrophobic segments. Note also that we cannot directly “see” the structure in the X-ray image; it records something akin to a Fourier transform and has to be processed to construct an averaged electron density map. The likelihood of different candidate structures is assessed by the degree they would match the observed density image.
PDB is a database that collects published protein structures. It is large, but still the structure of most proteins is not yet known. Since many proteins in one species are similar to related ones in other species (or in related proteins in the same organism), homology modeling can extrapolate an approximate 3-D structure.
Docking
Most often, PDB contains co-crystals of a protein with a ligand (native or drug compound). However, during the course of (virtual) high throughput screening and lead optimization, often millions of possible compounds are considered, and it is impossible to co-crystallyze each and every single one. Therefore, computational docking methods have been developed for predicting poses (the relative position of a ligand with respect to the protein, plus its internal conformation) of minimum binding free energy. The gold standard is a quantum-mechanical solution of the Schrödinger equation, but that is too computationally expensive except for the simplest cases. Although docking can be seen as a simpler, special case of the protein folding problem, it is still extremely hard.
All practical quantum- as well as classical mechanical approaches still have to make many simplifying assumptions. Classical models typically include a small number of force field types between atoms; most importantly, Coulomb (electrostatic) and van der Waals (“billiard ball”) interactions. Without going into too much detail, this equation sketches a general form of the potential function:
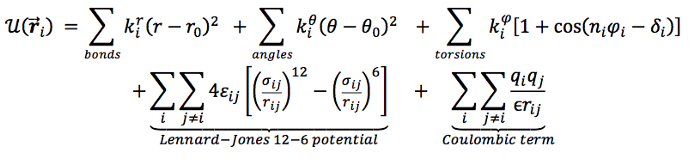
The computational complexity in docking arises from the combinatorial number of conformations of proteins and ligands; also, scores have to be calculated for all pairs of atoms. Molecular dynamics simulates motion over time, while molecular mechanics just tries to find a minimum energy state using Monte Carlo methods. Both types of methods rely on (often quite similar) force field functions.
Even the best scoring functions remain incomplete and approximate. It is often necessary to tune parameter sets for specific targets and applications. Traditionally, they have been classified into physical, empirical, and knowledge-based — the latter of which don’t even need to stick to physical descriptions, but are free to incorporate specific features and train weights to match experimentally observed data. It seems to me that these lines have become more blurred over time due to the influence of computing power and machine learning. There is a natural progression towards seeing these force fields as machine learning features, because at its core, what is machine learning other than parameter fitting? We will come back to this point shortly.
From Docking to Activity Prediction
Docking methods based on physically inspired force fields have proven themselves to do a reasonable job (in most cases) at identifying binding poses. But here lies another possible point of confusion. In principle, drug affinity is a physical consequence of the compound-protein interaction and governed by the same forces that give rise to the pose a molecule assumes; so, shouldn’t pose and affinity prediction be (almost) equivalent? Unfortunately and maybe confusingly, this is decidedly not the case. In fact, several studies [Li et al, 2014; Warren et al, 2006] found at most a very weak correlation between pose quality and measures of affinity and biological activity. As far as I can tell, the reasons are not entirely clear, but there is no scarcity of known pain points to blame:
- Imperfect force field approximations, particularly of non-additive polar effects
- Insufficient information about the state of the protein and the ligand before binding; the co-crystal only reflects the state afterwards.
- Missing or insufficient water modeling
- (Semi-)rigid protein models to keep computational complexity feasible. Sometimes the molecule “induces a fit” of a protein that would not be observed by itself.
- Crystal structure conformations differ from conformations at room temperature
- As already mentioned, proteins and molecules are flexible and constantly in motion. Rather than a single “minimum energy pose”, we are dealing with a statistical ensemble (Interestingly, an early approach [Dietterich et al, 1997] tried to apply multiple instance machine learning, where the input consists of sets of possible poses, and positive examples must contain at least one good pose).
- Missing or insufficient account of entropy
- And the ubiquitous noise in experimental labels and structures.
So, after we resign ourselves to the idea that computational docking alone is not sufficient for activity prediction, a natural thought is to build a rescoring function for the identified poses. Coming back to our previous observation that even physics-based force field scoring functions contain tuning parameters, we can treat the individual components as features in a ligand-based affinity model. Exactly this was realized in RF-score [Leung et al, 2015], an extension of the popular docking software Vina [Trott and Olson, 2010]. And why stop at those? So in a subsequent version [Leung et al, 2016], even more features were added in the form of counts of protein-ligand atom pairs types within fixed distance bins. RF-score was shown to outperform a pure docking model for predicting biological activity.
Let’s now move on to structural affinity prediction models that are not directly integrated with docking. Three broad classes can be distinguished: 3-dimensional generalizations of circular fingerprints, graph convolution, and grid-based representations.
3-D Fingerprints
We have seen how ECFP can map local atom neighborhoods of successively larger diameter into a fixed-size vector. We can generalize this idea by using, instead of bond structure neighborhoods, concentrically larger shells around an atom at multiples of a fixed base radius [Axen et al, 2017]. The hash function takes into account all atoms within a shell, whether bonded or not. In contrast to (standard) ECFP, such extended three-dimensional fingerprints (E3FPs) consider information pertaining not only to contiguously bound atoms, but also to nearby unbound atoms and to relative atom orientations (stereochemistry). In that paper, E3FPs were applied to molecules independently of proteins; therefore, a complication arises as to how many and which conformations to precompute. Since the Similarity Ensemble Approach (SEA) [Keiser et al, 2007] was a method already designed to work with sets of fingerprints, it seemed a natural fit. SEA identifies target similarities based on the sum of Tanimoto coefficients between two sets, normalized with the expected value of this statistic under the null hypothesis. Using E3FP, a few previously unknown off-target drug activities could be discovered and experimentally verified due to the complementarity of this metric to purely 2-dimensional ECFP.
Structural Protein−Ligand Interaction Fingerprints (SPLIF) [Da et al, 2014] are another instance in this class of representations. All compound and receptor atoms are identified that are close to each other, within some cutoff distance. Their neighborhood is expanded and hashed into a bit vector using regular 2-D circular fingerprints. in addition, the bits are annotated with the coordinates of the central atom. In the test phase, similarity of new molecules is determined by first applying Tanimoto distance, and then computing root mean square distance between the coordinates associated with the same bits. In a study on virtual screening on GPCRs [Lenselink et al, 2016], SPLIF compared favorably to a few other types of interaction fingerprints.
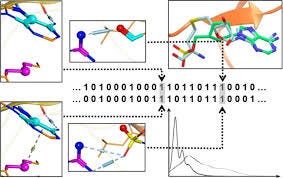
Schematic generation of SPLIF fingerprint.
Structural Graph Convolutions
We have described above the application of graph convolutions, a.k.a. neural message passing, to 2-D representations of molecules. This framework can be extended to incorporate spatial relationships. Let’s first look at applications for individual molecules. Here, researchers have had considerable success with what could be termed speedup learning.
Speed-Up Learning
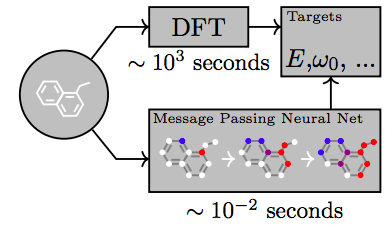
Modern quantum-mechanical methods are capable of calculating physical properties of molecules with very high accuracy. However, they are very slow and computationally expensive, and can only applied to a limited number of atoms. Therefore, one idea is to train a model to predict the quantum-mechanical outcome in one step; then, using the network in the place of the original physical model can result in huge speedups — up to 5 orders of magnitudes have been reported.
QM-9 is a database that exhaustively enumerates 134k stable small organic molecules made up to nine heavy atoms (C,O,N, and F). For each molecule, several properties and energies have been calculated using density functional theory (DFT). On this and similar databases, a variety of neural network models have been shown to be able to reach chemical accuracy [Faber et al, 2017]. The hope is that such models could also be able to extrapolate to molecules that are too large for full quantum-mechanical treatment.
In order to probe specific regions of an individual atom’s radial and angular neighborhood in a granular way, several basis functions have been proposed. These have some commonalities and differences, but to give you an idea of their form, let me focus on the work of Smith et al [2017]. For computational tractability, it is desirable to ignore interactions of atoms that are further away than some maximum distance. Additionally, for robustness, we want to avoid having large contributions near that cutoff. So in accordance with Behler-Parrinello symmetry functions, an envelope on the mutual distance R_ij of two atoms is defined,

A radial function with a learnable center and width is multiplied with the envelope, and these potentials are summed over all neighbor atoms,
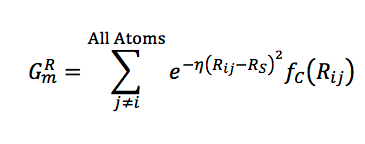
In a similar manner, angular properties between pairs of neighbors j,k can be captured:
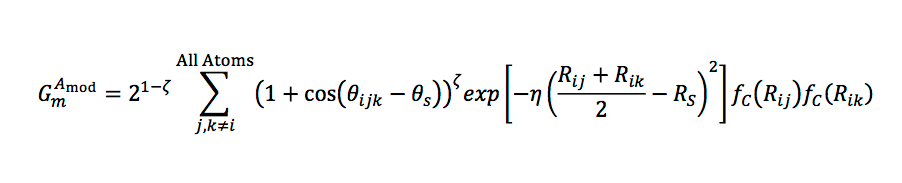
Smith et al [2017] showed that graph convolution with these radial basis functions achieves chemical accuracy on a 60K subset of the GDB-11 database with up to ten atoms.
So far, we have only discussed techniques dealing with single molecules. In contrast, Feinberg et al [2018] present a structural generalization of graph convolution that can be applied to protein-ligand complexes. To include bond and spatial information, the computation consists of three stages. The first one propagates only covalent bonds, exactly as in the 2-D case. For the second stage, a fixed number of edge types are extracted from the distance matrix of all protein-ligand atom pairs using thresholding; this phase propagates covalent and non-covalent edge types jointly. The third stage does a ligand-based graph gathering, again similar to the 2-D case. This work also improves on the edge function by employing gated recurrent units (GRU), which can better preserve long-distance dependencies. Spatial graph convolution fares well on PDBbind compared to a few baseline methods.
Grid-Based Approach
Atomwise, the company I work for, was first to apply deep convolutional neural networks to the domain of structural drug discovery [Wallach et al, 2015]. Instead of pixels in an image, a grid is constructed by interpolating the coordinates of a co-crystal of the receptor and the ligand. The grid consists of 20³ voxels spaced 1 Angstrom apart from each other, and centered on the binding site. Instead of 3 RGB channels, there are now many more channels, one for each atom type and possibly subtype. And instead of 2-D-convolutions, we employ 3-dimensional versions of these filters. Like in conventional image recognition, data is augmented by random rotations and translations. The overall AtomNet® technology's architecture resembles those used in image recognition; a number of convolutional layers of increasing width and decreasing resolution, followed by two fully connected layers and a sigmoid output layer for classification.
One compelling idea [Ragoza et al, 2017] is to use back-propagation through the network all the way to the initial ligand pose; the gradients can be interpreted as forces acting on the molecule to improve the docking pose. However, care has to be taken to avoid possible pitfalls. If the network has only seen “reasonable” training poses from crystal structures or docking, it might move ligands into positions where they clash with the protein, since it hasn’t learned to recognize them as physically impossible.
Rotation Equivariance

Translation equivariance means that a translation of the input of a layer results in a (mapping of) a likewise translation of the output for the original, untranslated, input. For convolutional networks, this property is baked into the form of the convolution operator. For natural images, translation equivariance is a natural feature; in addition, viewing an object at slight rotation angles should not change the interpretation too much either. However, we do not have complete rotation equivariance: recognizing a face upside-down is harder for animals. There are domains, though, where full rotation equivariance would be desirable, and the representation of molecules is one of them.
Any spatial features that are derived from pairwise atom distances are by definition translation and rotation equivariant. However, they have the weakness that they cannot distinguish mirror images; chiral molecules can often have very different biological effects. As a remedy, Thomas et al [2018] recently proposed tensor field networks, a form of graph convolution on a point cloud. The key idea consists in restricting convolutional filters to a particular separable functional form, where the angular part is a spherical harmonics, and the radial function is learnable.
No equivalent continuous rotation-equivariant form for the 3-D grid-based approach has been developed. However, several researchers suggested an approximation through discrete 90-degree-rotation equivariance [Dieleman et al, 2016]. Basically, two broad strategies exist: one cyclically rolls the filters of the network, while the other one cyclically rolls the input grid. Reported experiments include classification of galaxies, plankton, and aerial maps. However, to the best of my knowledge, none of these approaches has been applied directly to the drug discovery scenario.
Conclusion
In this post, I have tried to give a brief orientation to my fellow machine learning scientists who are new to the field of drug discovery. I apologize if I left out some works and references — There is a large body of literature and we can only scratch the surface here. Nevertheless, I hope to have sketched the main objectives, challenges and proposed machine learning approaches.
As we have seen, neural network approaches have had remarkable success in accurately predicting properties of isolated, small molecules, speeding up computation by many orders of magnitude compared to quantum-mechanical calculations. The hope is to push the boundary further out towards more and more complex chemical scenarios. What will it take to make significant progress in drug discovery? In my view, the most important resource needed is publicly available, high-quality affinity data. Accessibility of large, curated public datasets has been a major driving force in the success of the deep learning revolution. So far, databases of biological and chemical assays pale in comparison: ImageNet (2010 version) comprises 14 million images, while PDBbind (2017 version) contains 15 thousand protein-ligand complexes.
If academic researchers and pharmaceutical companies could share more of their internal data, the community as a whole would greatly benefit. As mentioned before, even publication of only unsuccessful experiments could help a lot. In addition, it is also important for the research community to settle on commonly agreed benchmarks and metrics that are able to capture prospective accuracy in real-world medicinal chemistry projects.
Drug discovery is hard. There must be reasons why despite decades of very smart people working on it, overall progress has been and still is vexingly slow! I don’t think it is realistic to expect that new machine learning algorithms by themselves, even deep learning, will completely solve all problems overnight.
Having said this, and maybe even because of the remaining challenges, it is an exciting field to work in as a machine learning scientist or software engineer. If you are playing with the thought of dipping your toe into it, don’t let a missing chemistry or biology background deter you — from my experience, absolutely, you can train convolutional neural networks on voxel representations without being familiar with the ins and outs of kinase conformations. It might be intellectually engaging (and monetarily rewarding) to invent new personalization strategies for advertisements. But working in life sciences gives you a shot at making a contribution for a longer life, and a life more worth living, for patients with cancer and other horrible illnesses.
References
- Axen, S. D., Huang, X. P., Cáceres, E. L., Gendelev, L., Roth, B. L., & Keiser, M. J. (2017). A Simple Representation of Three-Dimensional Molecular Structure. Journal of Medicinal Chemistry, 60(17), 7393–7409. https://doi.org/10.1021/acs.jmedchem.7b00696
- Ballester, P. J., & Mitchell, J. B. O. (2010). A machine learning approach to predicting protein-ligand binding affinity with applications to molecular docking. Bioinformatics (Oxford, England), 26(9), 1169–75. https://doi.org/10.1093/bioinformatics/btq112
- Cramer, R. D., Patterson, D. E., & Bunce, J. D. (1988). Comparative Molecular Field Analysis (CoMFA). 1. Effect of Shape on Binding of Steroids to Carrier Proteins. Journal of the American Chemical Society, 110(18), 5959–5967. https://doi.org/10.1021/ja00226a005
- Da, C., & Kireev, D. (2014). Structural protein-ligand interaction fingerprints (SPLIF) for structure-based virtual screening: Method and benchmark study. Journal of Chemical Information and Modeling, 54(9), 2555–2561. https://doi.org/10.1021/ci500319f
- Dahl, G. E., Jaitly, N., & Salakhutdinov, R. (2014). Multi-task Neural Networks for QSAR Predictions. Retrieved from https://arxiv.org/pdf/1406.1231.pdf
- Dieleman, S., De Fauw, J., & Kavukcuoglu, K. (2016). Exploiting Cyclic Symmetry in Convolutional Neural Networks. Retrieved from http://arxiv.org/abs/1602.02660
- Dietterich, T. G., Lathrop, R. H., & Lozano-Pérez, T. (1997). Solving the multiple instance problem with axis-parallel rectangles. Artificial Intelligence, 89(1–2), 31–71. https://doi.org/10.1016/S0004-3702(96)00034-3
- Duvenaud, D., Maclaurin, D., Aguilera-Iparraguirre, J., Gómez-Bombarelli, R., Hirzel, T., Aspuru-Guzik, A., & Adams, R. P. (2015). Convolutional Networks on Graphs for Learning Molecular Fingerprints. Neural Information Processing, 1–9. http://arxiv.org/abs/1509.09292
- Faber, F. A., Hutchison, L., Huang, B., Gilmer, J., Schoenholz, S. S., Dahl, G. E., … von Lilienfeld, O. A. (2017). Machine learning prediction errors better than DFT accuracy, 1–12. Retrieved from http://arxiv.org/abs/1702.05532
- Feinberg, E. N., Sur, D., Husic, B. E., Mai, D., Li, Y., Yang, J., … Pande, V. S. (2018). Spatial Graph Convolutions for Drug Discovery, 1–14. Retrieved from http://arxiv.org/abs/1803.04465
- Gabel, J., Desaphy, J., & Rognan, D. (2014). Beware of machine learning-based scoring functions — On the danger of developing black boxes . Beware of machine learning-based scoring functions — On the danger of developing black boxes. Journal of Chemical Information and Modeling, 54(Ml), 2807–2815. https://doi.org/10.1021/ci500406k
- Gilmer, J., Schoenholz, S. S., Riley, P. F., Vinyals, O., & Dahl, G. E. (2017). Neural Message Passing for Quantum Chemistry. Retrieved from http://arxiv.org/abs/1704.01212
- Gómez-Bombarelli, R., Wei, J. N., Duvenaud, D., Hernández-Lobato, J. M., Sánchez-Lengeling, B., Sheberla, D., … Aspuru-Guzik, A. (2016). Automatic chemical design using a data-driven continuous representation of molecules. ACS Central Science, 4(2), 268–276. https://doi.org/10.1021/acscentsci.7b00572
- Han, J., Zuo, W., Liu, L., Xu, Y., & Peng, T. (2016). Building text classifiers using positive, unlabeled and ‘outdated’ examples. Concurrency Computation, 28(13), 3691–3706. https://doi.org/10.1002/cpe.3879
- Hughes, J. P., Rees, S., Kalindjian, S. B., & Philpott, K. L. (2011). Principles of early drug discovery. British Journal of Pharmacology, 162(6), 1239–49. https://doi.org/10.1111/j.1476-5381.2010.01127.x
- Kadurin, A., Aliper, A., Kazennov, A., Mamoshina, P., Vanhaelen, Q., Khrabrov, K., & Zhavoronkov, A. (2016). The cornucopia of meaningful leads: Applying deep adversarial autoencoders for new molecule development in oncology. Oncotarget, 8(7), 10883–10890. https://doi.org/10.18632/oncotarget.14073
- Kearnes, S., Goldman, B., & Pande, V. (2016). Modeling Industrial ADMET Data with Multitask Networks. https://doi.org/1606.08793v1.pdf
- Kearnes, S., McCloskey, K., Berndl, M., Pande, V., & Riley, P. (2016). Molecular graph convolutions: moving beyond fingerprints. Journal of Computer-Aided Molecular Design, 30(8), 595–608. https://doi.org/10.1007/s10822-016-9938-8
- Keiser, M. J., Roth, B. L., Armbruster, B. N., Ernsberger, P., Irwin, J. J., & Shoichet, B. K. (2007). Relating protein pharmacology by ligand chemistry. Nature Biotechnology, 25(2), 197–206. https://doi.org/10.1038/nbt1284
- Kramer, C., Kalliokoski, T., Gedeck, P., & Vulpetti, A. (2012). The experimental uncertainty of heterogeneous public K_i data. Journal of Medicinal Chemistry, 55(11), 5165–5173. https://doi.org/10.1021/jm300131x
- Krizhevsky, A., Sutskever, I., & Hinton, G. E. (2012). ImageNet Classification with Deep Convolutional Neural Networks. Advances In Neural Information Processing Systems, 1–9.https://papers.nips.cc/paper/4824-imagenet-classification-with-deep-convolutional-neural-networks
- Lenselink, E. B., Jespers, W., Van Vlijmen, H. W. T. T., IJzerman, A. P., & van Westen, G. J. P. P. (2016). Interacting with GPCRs: Using Interaction Fingerprints for Virtual Screening. Journal of Chemical Information and Modeling, 56(10), 2053–2060. https://doi.org/10.1021/acs.jcim.6b00314
- Lenselink, E. B., Ten Dijke, N., Bongers, B., Papadatos, G., Van Vlijmen, H. W. T., Kowalczyk, W., … Van Westen, G. J. P. (2017). Beyond the hype: deep neural networks outperform established methods using a ChEMBL bioactivity benchmark set. Journal of Cheminformatics, 9(1), 1–14. https://doi.org/10.1186/s13321-017-0232-0
- Li, H., Leung, K. S., Wong, M. H., & Ballester, P. J. (2015). Improving autodock vina using random forest: The growing accuracy of binding affinity prediction by the effective exploitation of larger data sets. Molecular Informatics, 34(2–3), 115–126. https://doi.org/10.1002/minf.201400132
- Li, H., Leung, K. S., Wong, M. H., & Ballester, P. J. (2016). Correcting the impact of docking pose generation error on binding affinity prediction. In BMC bioinformatics (Vol. 8623). https://doi.org/10.1007/978-3-319-24462-4_20
- Li, Y., Han, L., Liu, Z., & Wang, R. (2014). Comparative assessment of scoring functions on an updated benchmark: 2. evaluation methods and general results. Journal of Chemical Information and Modeling, 54(6), 1717–1736. https://doi.org/10.1021/ci500081m
- Lopes, J. C. D., Dos Santos, F. M., Martins-José, A., Augustyns, K., & De Winter, H. (2017). The power metric: A new statistically robust enrichment-type metric for virtual screening applications with early recovery capability. Journal of Cheminformatics, 9(1), 1–11. https://doi.org/10.1186/s13321-016-0189-4
- Martin, E. J., Polyakov, V. R., Tian, L., & Perez, R. C. (2017). Profile-QSAR 2.0: Kinase Virtual Screening Accuracy Comparable to Four-Concentration IC50s for Realistically Novel Compounds. Journal of Chemical Information and Modeling, 57(8), 2077–2088. https://doi.org/10.1021/acs.jcim.7b00166
- Mysinger, M. M., Carchia, M., Irwin, J. J., & Shoichet, B. K. (2014). Directory of Useful Decoys, Enhanced (DUD-E): Better Ligands and Decoys for Better Benchmarking. Nucleic Acids Res, 42, 1083–1090.
- Ragoza, M., Turner, L., & Koes, D. R. (2017). Ligand Pose Optimization with Atomic Grid-Based Convolutional Neural Networks. Retrieved from https://arxiv.org/pdf/1710.07400.pdf
- Sanchez-Lengeling, B., Outeiral, C., Guimaraes, G. L., & Aspuru-Guzik, A. (2017). Optimizing distributions over molecular space. An Objective-Reinforced Generative Adversarial Network for Inverse-design Chemistry (ORGANIC). ChemRxiv, 1–18. https://doi.org/10.26434/chemrxiv.5309668.v3
- Smith, J. S., Isayev, O., & Roitberg, A. E. (2017). ANI-1: an extensible neural network potential with DFT accuracy at force field computational cost. Chem. Sci., 8(4), 3192–3203. https://doi.org/10.1039/C6SC05720A
- Thomas, N., Smidt, T., Kearnes, S., Yang, L., Li, L., Kohlhoff, K., & Riley, P. (2018). Tensor Field Networks: Rotation- and Translation-Equivariant Neural Networks for 3D Point Clouds. Retrieved from http://arxiv.org/abs/1802.08219
- Trott, O., & Olson, A. A. J. (2010). AutoDock Vina: improving the speed and accuracy of docking with a new scoring function, efficient optimization and multithreading. Journal of Computational Chemistry, 31(2), 455–461. https://doi.org/10.1002/jcc.21334.AutoDock
- Truchon, J.-F., & Bayly, C. I. (2007). Evaluating Virtual Screening Methods : Good and Bad Metrics for the “ Early Recognition ” Problem Evaluating Virtual Screening Methods : Good and Bad Metrics for the “ Early Recognition ” Problem, 47(February), 488–508. https://doi.org/10.1021/ci600426e
- Wallach, I., Dzamba, M., & Heifets, A. (2015). AtomNet: A Deep Convolutional Neural Network for Bioactivity Prediction in Structure-based Drug Discovery, 1–11. https://doi.org/10.1007/s10618-010-0175-9
- Wallach, I., & Heifets, A. (2018). Most Ligand-Based Classification Benchmarks Reward Memorization Rather than Generalization. Journal of Chemical Information and Modeling, 58(5), 916–932. https://doi.org/10.1021/acs.jcim.7b00403
- Warren, G. L., Andrews, C. V, Capelli, a, Clarke, B., LaLonde, J., Lambert, M. H., … Head, M. S. (2006). A critical assessment of docking programs and scoring functions. Capelli, J. Med. Chem., (49), 5912–5931. https://www.ncbi.nlm.nih.gov/pubmed/17004707
- Xu, Z., Wang, S., Zhu, F., & Huang, J. (2017). Seq2seq fingerprint: An unsupervised deep molecular embedding for drug discovery. … of the 8th ACM International Conference …, 285–294. Retrieved from http://dl.acm.org/citation.cfm?id=3107424
Related Posts
Subscribe
Stay up to date on new blog posts.
Atomwise needs the contact information you provide to send you updates. You may unsubscribe from these communications at any time. For information please review our Privacy Policy.